ML Aggarwal ICSE Class 9 Maths Ch-1 With Easy, Stepwise Solutions

MATHS CHAPTER – 1
Rational And Irrational Numbers
Exercise – 1.2

Have you ever wondered what kind of numbers we actually use in daily life? Some are neat and tidy—like fractions and whole numbers. Others are strange and never-ending—like √2 or π (pi). In this chapter, we’ll learn how to tell the difference between them by understanding rational and irrational numbers.

What Are Rational and Irrational Numbers?

Rational numbers are numbers that can be written as a fraction — that is, one number divided by another (as long as the denominator is not zero).
For example:

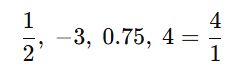
Even decimals that end (like 0.5) or repeat (like 0.333…) are rational.

On the other hand, irrational numbers cannot be written as exact fractions. Their decimal parts go on forever without repeating a pattern.

For example:

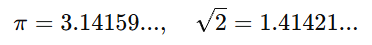
Why Is This Chapter Important?

Understanding rational and irrational numbers helps you:

• Know how the number system is structured
• Recognize patterns in decimals and roots
• Learn where common constants like √2 and π fit into math
• Build a strong base for algebra and higher-level topics

What You’ll Learn in This Chapter:

• Definition and examples of rational numbers
• Definition and examples of irrational numbers
• How to identify whether a number is rational or irrational
• Properties and differences between the two
• How they fit on the number line

Think of rational numbers as “friendly numbers” that can be written as fractions, and irrational numbers as “wild numbers” that go on forever with no repeating pattern.

By the end of this chapter, you’ll be able to spot the difference between them easily and understand how every number has its own place in the world of mathematics.