MATHS CHAPTER – 2
COMPOUND INTEREST
Exercise – 2.1
Introduction :
When we save money in a bank, invest in a fixed deposit, or borrow a loan, we often come across the term interest. You may already know about simple interest, where the interest is calculated only on the original amount (principal). But in real-life situations, especially in banking, investing, or long-term loans, compound interest plays a much more important role.
So, what is compound interest?
Imagine earning interest on your money and then earning interest on that interest! That’s the power of compound interest. It is a method of calculating interest not just on the initial principal, but also on the accumulated interest from previous periods. This process continues, and your money grows faster over time.
In this chapter, we will explore:
- What is compound interest and how it differs from simple interest
- The formula for compound interest and how to use it
- How compound interest applies in real life – in savings, investments, and loans
- Step-by-step examples and word problems to strengthen your understanding
By the end of this chapter, you will see how even small amounts of money can grow significantly over time — thanks to the magic of compounding. Let’s dive in and unlock one of the most powerful tools in the world of finance and mathematics!
What is Compound Interest and How It Differs from Simple Interest
Compound Interest (CI) is the interest calculated on the initial principal amount as well as the interest accumulated over previous periods. This means the interest for each time period is added to the principal before calculating the next period’s interest.
Simple Interest (SI), on the other hand, is calculated only on the original principal throughout the investment or loan duration, regardless of how much interest has been earned previously.
| Basis | Simple Interest (SI) | Compound Interest (CI) |
|---|---|---|
| Interest calculated on | Principal only | Principal + accumulated interest |
| Formula | SI = (P × R × T) / 100 | CI = P × [(1 + R/100)^T – 1] |
| Growth | Linear | Exponential |
| Common use | Short-term loans | Long-term savings/investments |
Example:
Let’s say you invest ₹1000 at 10% per annum for 2 years:
Simple Interest:
SI = (1000 × 10 × 2) / 100 = ₹200
Total Amount = ₹1000 + ₹200 = ₹1200
Compound Interest:
Year 1: Interest = ₹100 (10% of 1000), New Principal = ₹1100
Year 2: Interest = ₹110 (10% of 1100), Total = ₹1210
CI = ₹210 (more than SI)
The Formula for Compound Interest and How to Use It
The standard formula to calculate Compound Interest when interest is compounded annually is:
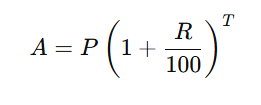
Where:
- A= Final Amount (Principal + Interest)
- P = Principal (initial amount)
- R = Annual interest rate (%)
- T = Time in years
To find only the Compound Interest (CI):
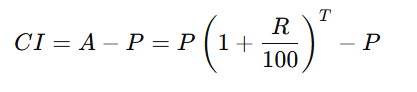
Example:
If ₹5000 is invested at 8% per annum compounded for 3 years:
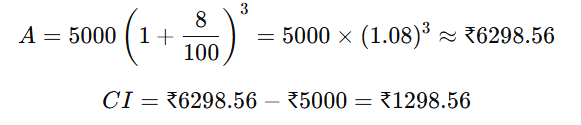
So, the interest earned is ₹1298.56 in 3 years.
How Compound Interest Applies in Real Life – in Savings, Investments, and Loans
Compound interest is widely used in the real world. Here are common applications:
🏦 Savings Accounts:
Banks offer compound interest on savings. The more often it’s compounded (annually, quarterly, monthly, or daily), the more you earn. Over time, your money grows significantly.
💰 Fixed Deposits / Investments:
Financial instruments like fixed deposits, mutual funds, and retirement accounts rely on compound growth. Reinvesting earnings allows your wealth to grow faster than with simple interest.
🏠 Loans and Mortgages:
In loans such as home loans or education loans, compound interest can work against you. The unpaid interest gets added to the loan amount, increasing your debt over time.
📈 Business Growth:
Even in business and finance, compound interest explains how profits can grow rapidly if reinvested wisely — often referred to as “the power of compounding.”










